Porque existe um sinal negativo no gradiente de pressão? Porque a aceleração produzida por um gradiente de pressão é direcionado de maneira oposta ao gradiente, assim o movimento da água associado " desce o gradiente": A equação que descreve os movimentos nos oceanos é derivada da segunda Lei de Newton, que expressa a conservação do momento na forma
força = massa vezes aceleração, ou
F = m a
(Aqui, os caracteres em negrito indicam vetores, os caracteres em itálico indicam escalares.)
Em fluídos essa equação é expressa em termos de forças por unidade de massa F' = F/ m, de forma quet
F' = dv / dt,
aqui v = (u,v,w) é a notação para o componente de velocidade ao longo dos respectivos eixos x,y,z com o eixo x apontando para o leste, o eixo y apontando para o norte e o eixo z apontando para baixo (a = dv/dt é a aceleração). Se existe mais do que uma força atuando, a segunda Lei de Newton se aplica ao somatório de todas elas. Essa Lei se aplica a um sistema de coordenadas absoluto, ou seja, o sistema está parado ou se move a uma velocidade constante. Os sistemas de coordenadas em oceanografia são em geral definidos com a sua origem em algum local da superfície terrestre (por exemplo, o pólo Norte). E assim, eles não estão parados ou se quer movendo a uma velocidade constante, e acompanham a rotação da Terra. Se a segunda Lei de Newton for aplicada nesses sistemas, temos que incluir uma força aparente ou virtual para levar o efeito da rotação da Terra em consideração. nota
| forças externas: (exercidas nos limites dos fluídos) | (a) forças (ou estresse) tangenciais (forças exercidas pelo vento) |
(b) efeitos guiados por diferenças termo-halinas (refriamento da superfície, evaporação, etc.)
| |
| forças internas: (exercidas em todas as parcelas de água) | (c) Campo de pressão interno (gradiente de pressão) |
| (d) Forças de maré |
| (a) | Fricção (difusão do momento) |
| (b) | Difusão da densidade (não é uma força, mas tem i efeito de mudar o gradiente de pressão) |
As forças 1a) e 1b) atuam apenas nos limites (interfaces ou contornos); matematicamente, elas é que vão determinar as condições de contorno para o problema geofísico mas não entram na equação de movimento. As forças 2a) atuam em todas as parcelas de água e portanto fazem parte da equação de movimento (ou seja, vão ser uma das forças que têm de ser somadas para a Lei de Newton). As forças 2b) não são forças atuando na movimentação das parcelas de água diretamente mas mudam os campos de temperatura e salinidade e portanto a densidade; seus efeitos são sentidos no campo de pressão.
Fazendo a soma de todas as forças atuando na segunda Lei de Newton para os oceanos, a mesma toma a seguinte forma
| aceleração da partícula= | - gradiente de pressão + força de Coriolis + força de maré por unidade de massa + fricção + gravidade |
A força da gravidade não atua como uma força horizontal e assim não pode produzir uma aceleração horizontal; ela é importante nos movimentos que envolvem deslocamentos verticais (convecção, ondas).
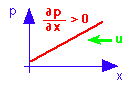
Porque existe um sinal negativo no gradiente de pressão? Porque a aceleração produzida por um gradiente de pressão é direcionado de maneira oposta ao gradiente, assim o movimento da água associado " desce o gradiente":
a pressão p aumenta com o aumento da distância x (para a direita), o gradiente de pressão é positivo, a aceleração é da pressão mais alta para a mais baixa, a corrente u flui descendo o gradiente (para a esquerda).
A força de Coriolis (assim chamada em honra ao engenheiro e matemático Gustave-Gaspard Coriolis, que a descreveu em 1835) é uma força aparente, ou seja, ela apenas aparece a um observador que se encontra num sistema de referência que está executando rotação. Para ver isso, considere uma pessoa sentado num carrossel em movimento, que está observando uma pessoa bem na sua frente lançando uma bola de fora do carrossel em sua direção. Conforme a bola se desloca, o carrossel gira, e a pessoa sentada nele tem de virar o rosto para continuar observando a bola, e conclui que deve haver uma força atuando na bola para que ela seja defletida de seu caminho linear. A pessoa que lança a bola, a vê atravessando um caminho linear e não nota a força que o observador em movimento concluiu que existisse. Ou seja, para o observador fora do carrossel, a deflexão no caminho da bola não existe, e portanto não existe a necessidade de uma força aparente para explicar o movimento da bola. Em oceanografia, as correntes são sempre expressas relativamente ao fundo oceânico - que executa a rotação junto da Terra - e portanto só pode ser explicada corretamente se uma força aparente for levada em consideração no somatório final de forças que atuam no movimento dos oceanos que é o efeito de Coriolis. A força de Coriolis é proporcional a magnitude da velocidade do fluxo e têm a direção perpendicular a direção do fluxo. Ela atua a esquerda do movimento no hemisfério sul e a direita do movimento no hemisfério norte. Uma maneira não muito correta, mas prática de se ver o porquê dessa diferença entre os hemisférios se relaciona ao princípio de conservação do momento angular.
Uma parcela de água em repouso no equador carrega um momento angular da rotação da Terra. Quando essa parcela se desloca em direção aos pólos ela carrega consigo seu momento angular mas ao mesmo tempo a sua distância do eixo de rotação é reduzido. Para conservar seu momento angular ela tem de aumentar sua rotação em torno do eixo, da mesma forma que bailarinas podem aumentar sua velocidade de rotação trazendo os braços mais próximos ao seu corpo (trazendo mais massa em direção ao eixo de rotação). A partícula começa, assim, a girar mais rápido que a rotação da Terra abaixo dela, quer dizer se move em direção a leste. Isso resulta em uma deflexão no caminho linear para a direita no hemisfério norte e para a esquerda no hemisfério sul. Da mesma forma, uma parcela de água saindo dos pólos em direção ao equador vai aumentar sua distância do eixo de rotação e para conservar momento angular tem de diminuir a sua velocidade de rotação em relação a da Terra abaixo; assim, começa a se mover em direção a oeste o que de novo vai representar uma deflexão a direita no hemisfério norte e a esquerda no hemisfério sul.
O efeito da rotação no movimento aparente de objetos pode ser facilmente demostrado em experimentos de labortório. Você pode ver um exemplo desses na seguinte animação .
Se algum momento é dado a uma parcela de água (ou seja, ela é empurrada) e depois, a mesma parcela é deixada de lado, a única força atuando é a de Coriolis. A segunda Lei de Newton diz que a parcela irá acelerar em uma taxa constante. Desde que aceleração é produzida pela força aparente de Coriolis a mesma tem o sentido perpendicular ao caminho da parcela; ou seja; a aceleração toma uma forma de uma constante mudança de direção. O movimento inercial é muito comum no oceano, e é geralmente encontrado de forma superposta a outro movimento (como o geostrófico ou o forçado pelo vento discutidos abaixo). A figura 6.1 nos dá um exemplo para o Mar Báltico.
No interior dos oceanos, i.e., abaixo dos 100 metros de profundidade e mais de 100 km de distância da costa, as forças de fricção podem ser desprezadas. A circulação em equilíbrio é assim determinada pelo balanço entre as forças de gradiente de pressão e o efeito de Coriolis. Essa balanço é conhecido como fluxo geostrófico. Num fluxo geostrófico as partículas se movem ao longo de linhas isobáricas (contornos com pressão constante), com alta pressão a sua esquerda no hemisfério sul, e a sua direita no hemisfério norte. Desde que a pressão é determinada pelo peso de água acima, altas e baixas pressões são equivalentes a altos e baixos níveis do mar. O fluxo geostrófico é portanto relacionada ao formato da superfície dos oceanos.
A força de Coriolis e a força do gradiente de pressão atuam em todas as partículas de água. O fluxo geostrófico é portanto parte integrante das correntes oceânicas em todas as profundidades e locais. Abaixo dos 100 metros de profundidade e a cerca de 100 km de distância da costa, todas as correntes são geostróficas; próximas a superfície e perto de limites de contornos elas são modificadas por forças adicionais.
A figura 6.2 mostra um exemplo de fluxo geostrófico no sistema de correntes equatoriais. Note que as variações do nível do mar são apenas da ordem de 0,2 a 0,4 metros. Essas variações pequenas são impossíveis de observar no oceano aberto. Elas tem sido, entretanto, verificadas em estreitos, aonde o reverso da corrente fluindo através do estreito produz uma reversão na inclinação da superfície da água no estreito. A inclinação pode ser medida com medidores de nível do mar instalados nos dois extremos do estreito.
Um outro aspécto importante do fluxo geostrófico se relaciona com a circulação em torno de vórtices. Afigura 6.3 mostra o princípio. Ele se aplica igualmente a vórtices oceânicos e atmosféricos e explica porque um sistema de alta pressão a leste de Adelaide na Austrália do Sul trás ventos do quadrante norte.
As correntes nos primeiros 150 metros dos oceanos aproximadamente são diretamente afetadas pelo vento, i.e., pela transferência de momento da atmosfera para o oceano. O balanço entre as forças portanto envolve forças de fricção, que faz com que as condições não sejam mais aquelas de um fluxo geostrófico; a água se moverá ao longo de linhas de mesma pressão desde de regiões de alta pressão até regiões de baixa pressão. A camada em que o fluxo não é geostrófico é conhecida como camada de Ekman. A direção do movimento da água varia com a profundidade. Os detalhes são complicados (figura 6.4); mas quando apenas uma situação de equilíbrio é considerada, um resultado importante é que o transporte líquido (i.e, médio com a profundidade) na camada de Ekman é direcionado perpendicularmente a direção do vento, para a esquerda no hemisfério sul e para a direita no hemisfério norte.
Ressurgência é o processo de movimentação vertical de massas de água para a superfície dos oceanos. Zonas de ressurgência costeiras e equatoriais são respostas dos ventos predominantes e nos dão evidência direta da dinâmica de transporte de Ekman. Um terceiro tipo de ressurgência não é direcionada pelo vento; ocorrendo no Oceano Austral, sendo um dos elementos da circulação termohalina global.
© 1996 - 2000 M. Tomczak. Last updated 5/1/2000contact address: