The Hardy-Weinberg Law states that in a genetically steady state the frequency distribution of gene alleles in a population remains constant.
The principle can be demonstrated with a population that carries only one gene with the alleles M and N, for example blood types, as found in most human populations. Assume that the population consists of 49% individuals of blood type M, 9% of blood type N and 42% of blood type MN. This corresponds to 49% homozygotes of type MM, 9% homozygotes of type NN and 42% heterozygotes of type MN.
The gene pool of the population consists of 70% alleles of type M (all alleles from the MM group and half the alleles from the MN group, ie 49% + 21%) and 30% alleles of type N (all alleles from the NN group and half the alleles from the MN group, ie 9% + 21%). Because gametes receive only one allele during formation, this 70:30 ratio is also the distribution of sex cells in the population. The ratio can be expressed as 0.7:0.3 if the population size is normalized to 1.
Under conditions of random mating the next generation will consist of
It is seen that the final result is a distribution of 49% type M, 42% type N and 9% type MN, the same as the parent population.
Expressed in mathematical form the Hardy-Weinberg Law is: If the ratio of two alleles M and N in a gene pool is p:q the distribution of the genotypes is given by
p2 + 2 pq + q2 = 1
where p2 represents the genotype MM, 2 pq the genotype MN and p2 the genotype NN. It shows that every allele ratio is associated with a corresponding genotype distribution:
| allele ratio M : N |
genotype distribution MM : NN : MN |
| 80% : 20% | 64% : 4% : 32% |
| 70% : 30% | 49% : 9% : 42% |
| 60% : 40% | 36% : 16% : 48% |
| 50% : 50% | 25% : 25% : 50% |
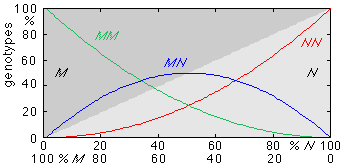
The figure below gives the law in graphical form; the dark shaded half indicates the percentage of M alleles, the light shaded half the percentage of N alleles and the lines the resulting genotypes:
