The basis for electromagnetic wave theory
The description of electromagnetic radiation or EMR in physics underwent several changes. The Arabian scientist Alhazen (965 Ð 1039) explained the properties of radiation through ray theory. In 1865 Maxwell formulated his set of equations which is based on a description of EMR as waves. Wave theory was known before Maxwell; but it was then always applied in the context of waves propagating through a medium (water waves cannot propagate without water), which led to the erroneous concept of "aether" as the medium for EMR propagation. However, Maxwell's formulation of the unified theory of electricity and magnetism does not mention a medium, and this encouraged others to think beyond wave theory and led to the discoveries of Planck in 1900 and EInstein in 1905.
Let FE be the force between two electrical charges q1 and q2 separated by a distance r. In a vacuum this force is found by observation to be
FE = q1 q2/r2
The proportionality constant is found from experiment; it is 4¹.e0, where e0 is called the permittivity in free space. The magnitude of the force per unit charge FE/q is called the electric intensity and denoted by E.
Similarly, the magnitude of a magnetic force FH on a particle moving with a velocity v through a magnetic field m0, where m0 is the permeability in vacuum, is found from experiment to be
FH = q v sinQ m0H
where Q is the angle between the magnetic intensity field vector and the velocity vector.
The relationship between H and E was investigated by Gauss, Faraday, Ampère, Ohm and others and finally formulated in 1864 by Maxwell who combined the various relationships into what is now known as Maxwell's equations:
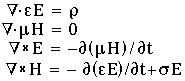
The first of these equations is known as Gauss' Law of Electricity, the second as Gauss' Law of Magnetism, the third as Faraday's Law and the last one as Ampère's Law, modified by Maxwell. r is the electric charge density. s is the conductivity of the medium (s = 0 in free space). The following list summarizes the terms and symbols in the equations: