The graph below illustrates the difference between geometric and arithmetic progression. Arithmetic progression means that a quantity increases linearly as time proceeds; geometric progression means that it increases as the square of time. Malthus' theory claims that populations always tend to increase in geometric progression, while the means of subsistence increase in arithmetic progression. Population growth is then limited through shortage of subsistence.
In the example the assumption is that initially the means of subsistence are sufficient to support the population but are outstripped in the fourth generation. The numerical example is built on s = 0.25 . 2x.
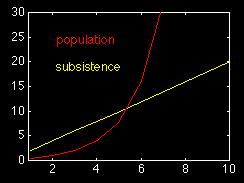
p: population s: subsistence s p ---------- 1 0.5 2 1 3 2 4 4 5 8 6 16 7 32 8 64 9 128 10 256