Consider a body that moves as indicated by the yellow curve: It starts at 15 m from the origin, moves towards the origin for nearly a second, then moves away for about 2 seconds and finally moves back towards the origin at increasing speed, where it arrives after a total time of 5 seconds. What is its speed at any particular instance in time, for example after 2 seconds?
Speed is distance travelled divided by time. To find the speed at the instance 2 s, we can measure the distance Dx and the corresponding time interval Dt and divide Dx by Dt:
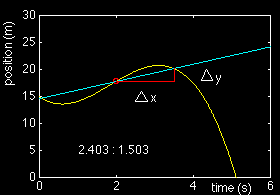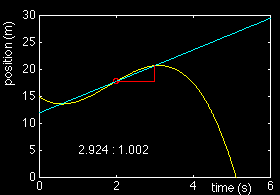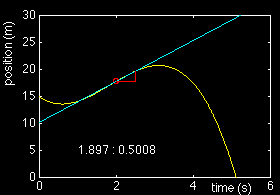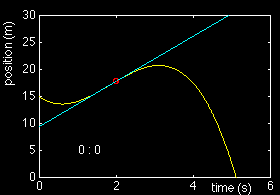
v = Dx / Dt

As can be seen from the graph, the value of Dx/Dt depends on how large or small we choose Dx to be. The most accurate value is obviously obtained when Dx approaches zero, because it is then when the change of position with time along the straight line defined by Dx / Dt is identical to the change of position with time of the yellow curve. The following table gives the successively better estimates for the speed:
| distance (m) | elapsed time (s) | estimated velocity (m/s) |
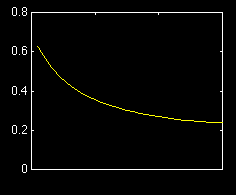
1.503 2.403 0.625 1.452 2.544 0.571 1.402 2.664 0.526 1.352 2.763 0.489 1.302 2.841 0.458 1.252 2.900 0.431 1.202 2.940 0.409 1.152 2.962 0.389 1.102 2.966 0.372 1.052 2.953 0.356 1.002 2.924 0.343 0.952 2.880 0.330 0.902 2.821 0.320 0.851 2.748 0.310 0.801 2.661 0.301 0.751 2.562 0.293 0.701 2.451 0.286 0.651 2.328 0.280 0.601 2.194 0.274 0.551 2.050 0.269 0.501 1.897 0.264 0.451 1.735 0.260 0.401 1.566 0.256 0.351 1.389 0.252 0.301 1.205 0.249 0.250 1.015 0.247 0.200 0.820 0.244 0.150 0.620 0.242 0.100 0.417 0.241 0.050 0.210 0.239 0.000 0.000 ? |
||
The last value should be the accurate value. But division through zero is an undefined mathematical operation, because it can produce any value. (This is easily seen if we imagine that we repeat the same operation - a sequence of Dx / Dt - at another instance of time, for example at 3 s. The sequence will be different, but it will again end in zero divided by zero.) On the other hand, a plot of the speed estimates indicates that they converge towards the final correct value:
a plot of the data in the last column
Newton and Leibnitz developed the method to correctly determine the limit of any sequence Dx / Dt as Dx and Dt go to zero. Their method is known as calculus (German Differentialrechnung, French calcul différentiel).