Conic sections are mathematical curves that result if two right circular cones that stand on each other's points are intersected by a plane. Two stellar bodies interacting with each other through gravity travel on paths described by a conic section.Conic sections are mathematical curves that result if two right circular cones that stand on each other's points are intersected by a plane. Two stellar bodies interacting with each other through gravity travel on paths described by a conic section.
The are four conic section curves:
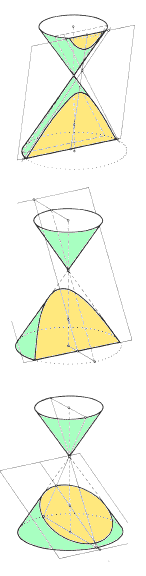
A hyperbola is generated when the plane cuts through both cones (top figure).
A parabola is generated when the plane cuts through the cones at an angle parallel to one side of the cones and the cut therefore goes only through one of the cones (middle figure).
An ellipse is generated when the plane cuts through the cone at an angle closer to horizontal, so that the intersection produces a closed contour (bottom figure).
A circle is a special case of the ellipse when the plane cuts through the cone exactly perpendicular to the cone's axis (in this case horizontally; not shown).
Asteroids and comets travel on hyperbolic, parabolic or elliptic orbits. Those on hyperbolic or parabolic orbits reach us from space, are only seen once and disappear again into space.
Planets revolve around the sun and therefore travel on elliptical orbits.
In mathematical notation the conic sections are given by
hyperbola: x2/a2 - y2/b2 = 1
parabola: y2 = 2px.
ellipse: x2/a2 + y2/b2 = 1
based on Schell, C., J. Krummenacher and O. Bieri: Zirkelkonstruktionen des Mascheroni, Angewandte Mathematik. http://www.oliver-bieri.ch/mascheroni/geschichte.htm (accessed 4 February 2004)