The model is based on the linearised vertically integrated Equations of Motion and the continuity equation in the form derived in the theory page:
A co-oscillation tide is a standing wave generated by tidal movement at the open end of the basin or gulf. The two unknowns ζ and q can therefore be written as
where ω< is the frequency of a tidal constituent. Introducing these forms for the unknowns into the equations gives a set of coupled equations for Z and Q:
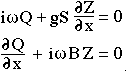
These equations can be solved numerically if the width B and the cross-sectional area S vary only slowly in x. The gulf or basin is divided into sections of length Δx, and the equations are written in finite difference form:

The computation begins at the head of the gulf with Q0= 0 and Z1 = 1, and Q and Z are evaluated at alternate sections.
The effect of bottom friction on the tidal wave can be incorporated through a linear damping term. If friction is assumed to be proportional to the bottom velocity, which is proportional to the transport q, the vertically integrated equations become
where r is a friction parameter; 1/r corresponds to the time over which the tidal amplitude would decrease to 1/e of its original value if the tidal forcing would be switched off. The finite difference equations are then

| continue with example |
back to co-oscillation tides |
This utility is based on A. K. Easton (1978) A reappraisal of the tides in Spencer Gulf, South Australia. Australian Journal of Marine and Freshwater Research 29, 467 - 477.
Last updated 23 August 2000. Contact address: